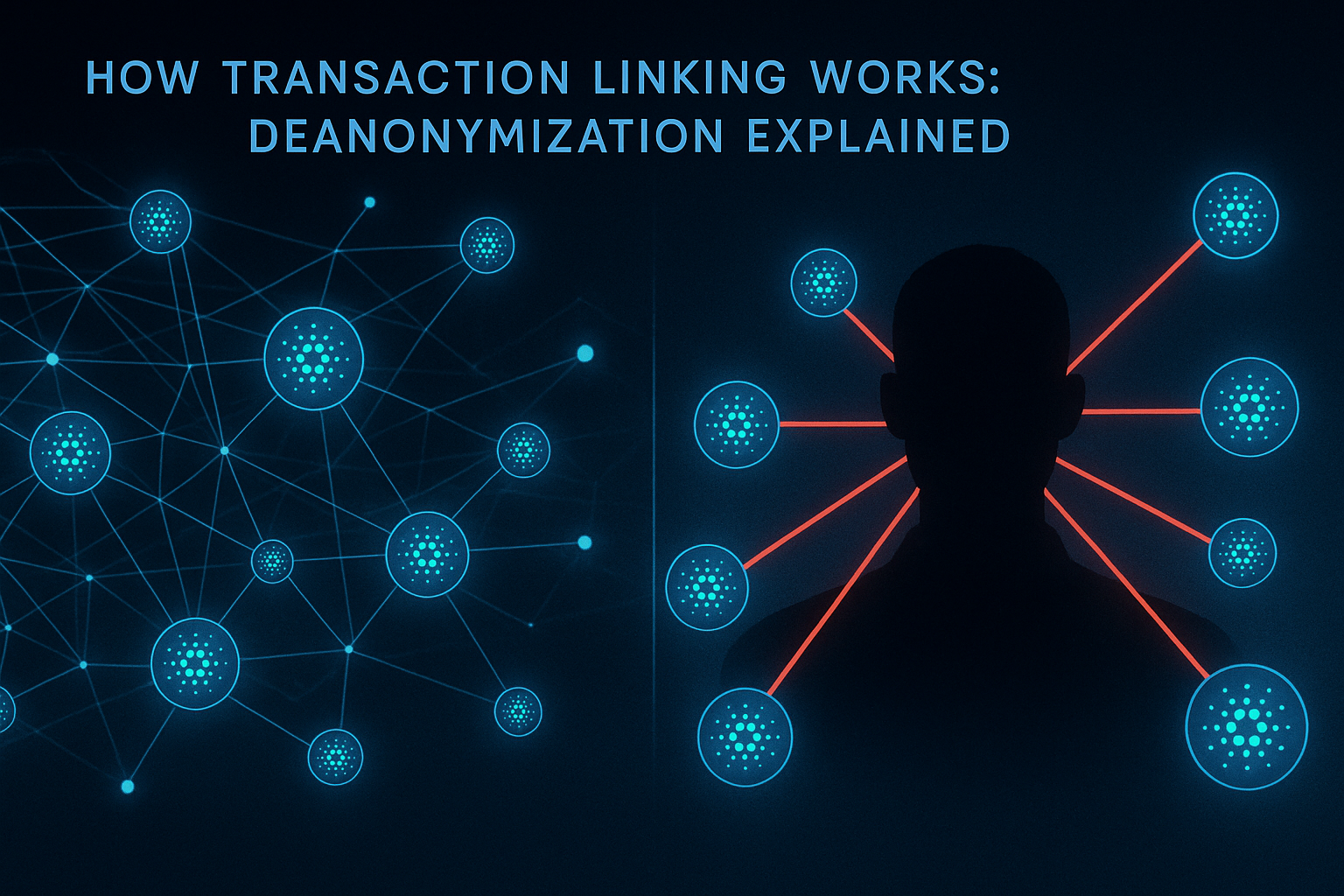
Cryptographic Methods Behind Transaction Mixing
Dive deep into the cryptographic foundations of transaction mixing, exploring encryption methods, zero-knowledge proofs, and security protocols that ensure mixing anonymity.
Cryptographic Foundations of Mixing
Transaction mixing relies on sophisticated cryptographic techniques to ensure anonymity and security. These methods form the mathematical backbone that makes it possible to break transaction links while maintaining verifiability and preventing fraud.
The cryptographic security of mixing systems depends on several key principles: computational hardness assumptions, zero-knowledge proofs, and secure multi-party computation protocols. Understanding these foundations is crucial for evaluating the security guarantees of any mixing system.
Mathematical Foundations
Modern mixing systems are built on well-established cryptographic primitives:
- Elliptic Curve Cryptography: For digital signatures and key exchange
- Hash Functions: For commitment schemes and random number generation
- Zero-Knowledge Proofs: For privacy-preserving verification
- Secure Multi-Party Computation: For collaborative mixing protocols
"The security of mixing systems depends not on obscurity, but on the mathematical hardness of well-studied cryptographic problems."
Digital Signatures in Mixing
Digital signatures are fundamental to mixing systems, providing authentication and non-repudiation while maintaining privacy. The choice of signature scheme significantly impacts both security and privacy properties.
ECDSA and Schnorr Signatures
Most mixing systems use elliptic curve digital signature algorithms:
- ECDSA: Widely used in Bitcoin and other cryptocurrencies
- Schnorr Signatures: More efficient and privacy-friendly
- EdDSA: High-performance signature scheme
- BLS Signatures: Aggregate signatures for efficiency
Ring Signatures
Ring signatures are crucial for privacy-preserving mixing protocols:
- Group signature schemes
- Threshold signature protocols
- Anonymous credential systems
- Plausible deniability guarantees
Commitment Schemes
Commitment schemes are essential for mixing protocols, allowing participants to commit to values without revealing them until later. This enables secure multi-party mixing without requiring trust in a central authority.
Pedersen Commitments
Pedersen commitments are widely used in mixing systems:
- Homomorphic properties
- Perfect hiding
- Computational binding
- Efficient verification
Merkle Tree Commitments
Merkle trees provide efficient commitment schemes for large datasets:
- Logarithmic proof size
- Efficient verification
- Batch commitment support
- Incremental updates
Zero-Knowledge Proofs
Zero-knowledge proofs are the cornerstone of privacy-preserving mixing systems. They allow participants to prove knowledge of certain information without revealing the information itself.
zk-SNARKs (Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge)
zk-SNARKs are widely used in privacy-preserving systems:
- Succinct proof size
- Non-interactive verification
- Universal setup requirements
- Trusted setup ceremonies
zk-STARKs (Zero-Knowledge Scalable Transparent Arguments of Knowledge)
zk-STARKs offer advantages over zk-SNARKs:
- No trusted setup required
- Quantum-resistant
- Transparent verification
- Scalable proof generation
Bulletproofs
Bulletproofs are efficient zero-knowledge proofs for range statements:
- No trusted setup
- Efficient range proofs
- Confidential transactions
- Batch verification
Secure Multi-Party Computation (MPC)
MPC protocols enable multiple parties to compute functions over their inputs while keeping those inputs private. This is essential for decentralized mixing systems where no single party should have access to all information.
Threshold Cryptography
Threshold cryptography allows distributed key generation and signing:
- Distributed key generation
- Threshold signature schemes
- Robust protocols
- Fault tolerance
Secret Sharing
Secret sharing schemes distribute sensitive information among multiple parties:
- Shamir's Secret Sharing
- Verifiable secret sharing
- Proactive secret sharing
- Dynamic secret sharing
Homomorphic Encryption
Homomorphic encryption allows computation on encrypted data without decrypting it. This is crucial for privacy-preserving mixing systems where computations must be performed on sensitive data.
Partially Homomorphic Encryption
Partially homomorphic schemes support specific operations:
- Additive homomorphism
- Multiplicative homomorphism
- Efficient computation
- Practical applications
Fully Homomorphic Encryption
Fully homomorphic encryption supports arbitrary computations:
- Universal computation
- High computational overhead
- Recent efficiency improvements
- Future potential
Random Number Generation
Cryptographically secure random number generation is essential for mixing systems. The quality of randomness directly impacts the security and privacy properties of the system.
Cryptographically Secure PRNGs
Secure random number generation requires:
- Cryptographically secure algorithms
- Proper entropy sources
- Seed management
- Periodic reseeding
Distributed Randomness
Distributed randomness generation prevents single points of failure:
- Multi-party randomness
- Verifiable random functions
- Beacon-based randomness
- Threshold randomness
Mixing Protocol Cryptography
The cryptographic design of mixing protocols determines their security and privacy properties. Different protocols use different combinations of cryptographic techniques.
CoinJoin Cryptography
CoinJoin protocols use specific cryptographic techniques:
- Multi-signature schemes
- Commitment schemes
- Zero-knowledge proofs
- Secure communication
Decentralized Mixing Cryptography
Decentralized mixing requires more sophisticated cryptography:
- Secure multi-party computation
- Threshold cryptography
- Byzantine fault tolerance
- Consensus mechanisms
Privacy-Preserving Verification
Mixing systems must provide verifiability without compromising privacy. This requires sophisticated cryptographic techniques that allow verification of system properties without revealing sensitive information.
Range Proofs
Range proofs allow verification that values are within specified ranges:
- Amount verification
- Balance proofs
- Confidential transactions
- Privacy preservation
Membership Proofs
Membership proofs verify that values belong to specific sets:
- Anonymity set verification
- Group membership proofs
- Eligibility verification
- Privacy-preserving authentication
Security Analysis
The security of mixing systems depends on the cryptographic assumptions underlying their protocols. Understanding these assumptions is crucial for evaluating system security.
Computational Assumptions
Mixing systems rely on well-established computational assumptions:
- Discrete logarithm problem
- Elliptic curve discrete logarithm
- RSA assumption
- Learning with errors
Security Models
Security analysis requires formal security models:
- Semantic security
- Indistinguishability
- Non-malleability
- Adaptive security
Implementation Considerations
Implementing cryptographic mixing systems requires careful attention to several factors:
Performance Optimization
Cryptographic operations can be computationally expensive:
- Algorithm optimization
- Hardware acceleration
- Parallel processing
- Efficient protocols
Side-Channel Resistance
Implementation must resist side-channel attacks:
- Timing attacks
- Power analysis
- Cache attacks
- Electromagnetic analysis
Future Cryptographic Developments
The future of mixing cryptography looks promising with several exciting developments:
Post-Quantum Cryptography
Quantum computing threatens current cryptographic systems:
- Lattice-based cryptography
- Code-based cryptography
- Multivariate cryptography
- Hash-based signatures
Advanced Zero-Knowledge Proofs
Future developments will focus on more efficient zero-knowledge proofs:
- Universal zk-SNARKs
- Recursive composition
- Batch verification
- Hardware acceleration
Privacy-Preserving Machine Learning
Machine learning can enhance mixing systems:
- Privacy-preserving analytics
- Federated learning
- Differential privacy
- Secure aggregation
The cryptographic methods behind transaction mixing represent some of the most sophisticated applications of modern cryptography. By combining multiple cryptographic techniques, mixing systems can provide strong privacy guarantees while maintaining security and verifiability. As cryptographic research continues to advance, we can expect to see even more sophisticated mixing protocols that provide stronger privacy guarantees with better performance.